Nos sites
eServices
 Connexion
Connexion
 Connexion
Connexion

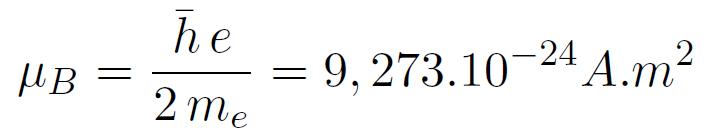
Où 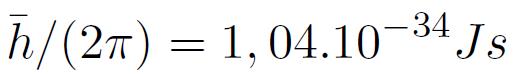
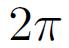
A cette première contribution s'ajoutent les moments cinétique et magnétique de Spin, correspondant de manière imagée au mouvement de rotation de l'électron sur lui-même. On note que dans le référentiel de l'électron, le mouvement du noyau crée un champ magnétique qui va donc interagir avec le moment magnétique de Spin de l'électron : il s'agit du couplage Spin Orbite
Pour les atomes présentant des orbites électroniques « pleines », les moments se compensent globalement. Dans certains cas liés à l'existence de sous-couches incomplètes, la compensation des moments n'est pas totale et l'atome est magnétique.Dans le cadre du couplage de Russel-Saunders, pertinent pour les éléments du groupe du fer (couche incomplète 3d) et des éléments de la série des Terres rares (couche incomplète 4f) qui nous concernent essentiellement, le moment magnétique résultant de l'atome isolé se détermine de la manière suivante :
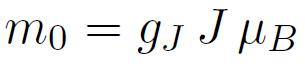
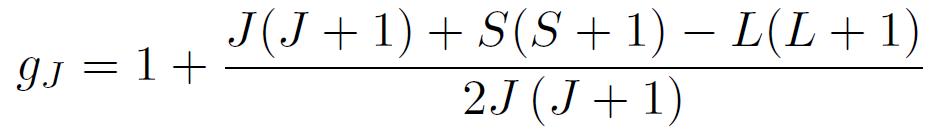
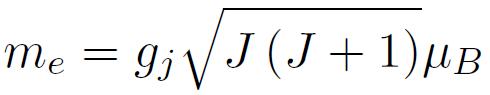 quantité reliée à la température de Curie. C'est le moment effectif qui figure dans le tableau 2. Dans une description classique des propriétés magnétiques de l'atome isolé, mo et me coïncident.
quantité reliée à la température de Curie. C'est le moment effectif qui figure dans le tableau 2. Dans une description classique des propriétés magnétiques de l'atome isolé, mo et me coïncident.Dans ces conditions, seuls les éléments dont les électrons responsables du magnétisme appartiennent à des couches internes et donc « protégées » sont capables de préserver leur caractère magnétique au sein d'un édifice. C'est le cas des éléments du groupe du fer (couche incomplète 3d) et des éléments de la série des Terres rares (couche incomplète 4f) et c'est à leur seule étude qu'on se consacrera.
On s'attend pour ces éléments à trouver des propriétés magnétiques à l'état condensé proches de ce que prévoit le magnétisme des atomes à l'état libre. Surgit alors une nouvelle difficulté : il s'agit, pour les matériaux conducteurs du groupe du fer, du fait que la sous-couche 3d, comme la sous-couche 4s, forme une bande de conduction. On est alors amené à considérer collectivement le remplissage des sous-couches 3d et 4s, elles-mêmes décomposées en demi-bandes (3d-, 3d+, 4s-, 4s+). Le moment magnétique de l'atome résulte de l'écart de remplissage des sous-couches 3d- et 3d+ lorsque tous les électrons ont été casés (cf tableau 1) et n'a plus rien à voir avec les propriétés de l'atome libre. Ce magnétisme est dénommé magnétisme itinérant et décrit dans le cadre du modèle de Stoner qui ne sera pas étudié ici.
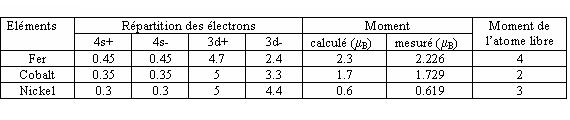
On ne rencontre pas la même difficulté avec les métaux de Terres rares, car dans ce dernier cas la conduction électrique et la cohésion métallique sont assurées par des électrons qui participent peu au moment magnétique de la substance.
On peut néanmoins rester dans le cadre du magnétisme localisé même avec les éléments du groupe du fer quand ceux-ci sont à l'état ionique. Cela concerne par exemple les oxydes, dont la très importante classe des ferrimagnétiques. Sont également concernées les Terres rares et tous leurs composés. On obtient alors les résultats regroupés dans le tableau 2.
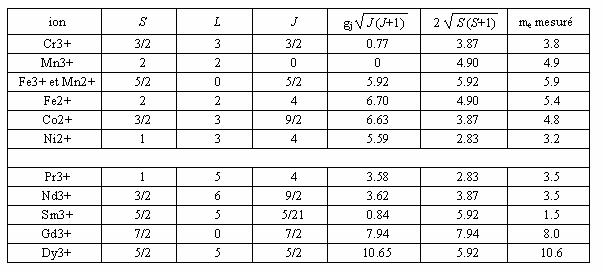
On constate que si l'accord entre théorie et mesure est excellent pour les ions de Terres rares, il l'est beaucoup moins pour les ions du groupe du fer pour lesquels tout se passe comme si le moment orbital était nul. Cela provient de l'interaction électrostatique entre les orbitales des électrons responsables du magnétisme de l'atome et du champ électrique lié à la distribution de charges de l'environnement et dénommé champ électrique cristallin (cf figure 1). Cet effet se manifeste de manière imagée, par une déformation des trajectoires électroniques qui tendent à s'approcher ou à éviter les atomes voisins.
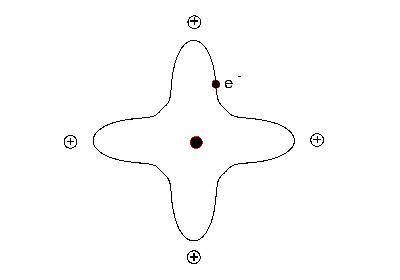
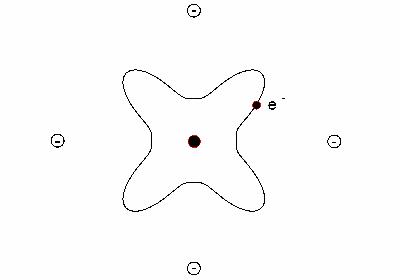
Figure 1 : Interaction de champ cristallin : lorsque les charges des atomes voisins sont positives, les trajectoires électroniques s'approchent des atomes (à gauche). Au contraire, lorsque ces charges sont négatives, les trajectoires évitent les atomes voisins.
Pour expliquer les conséquences de cet effet, on recourt à la mécanique quantique qui enseigne que les électrons d'une sous-couche donnée peuvent occuper un nombre m d'orbitales distinctes, où m désigne le nombre magnétique quantique de l'électron considéré. Pour l'atome isolé, la résultante présente une symétrie sphérique avec un moment orbital résultant donné. En fonction de la symétrie du cristal et de l'environnement (champ cristallin), certaines orbitales sont favorisées et le moment orbital résultant changé.
Dans le cas particulier très important des électrons 3d, on a m=5 orbitales possibles. Dans un environnement de symétrie cubique, les cinq orbitales correspondant à l'état libre se combinent pour donner cinq nouvelles orbitales qui se répartissent en deux groupes, dont l'un présente un moment orbital nul (de manière plus exacte, c'est la valeur de la projection du moment sur un axe quelconque dont il s'agit). On observe souvent que c'est celui-ci qui est favorisé. Une conséquence très importante est une forte diminution du moment orbital de l'atome, qui peut même aller jusqu'à s'annuler. On dit alors, de manière impropre, que le moment cinétique orbital est bloqué (« quenched » en anglais).
L'effet de champ cristallin est d'autant plus important que les électrons responsables du magnétisme de l'atome sont directement sous l'influence des ions environnants. La situation vécue par les éléments dont les électrons responsables du magnétisme appartiennent à la sous-couche 3d diffère ainsi radicalement de la situation vécue par les éléments 4f, les électrons de cette dernière bénéficiant de l'effet d'écrantage réalisé par les nombreuses sous-couches externes 5s, 5p, 6s, au contraire des éléments 3d seulement protégés par la sous-couche 4s.
Il apparaît donc que les effets de champ cristallin seront primordiaux pour les éléments du groupe du fer, conduisant souvent à une forte diminution du moment orbital (et donc à la disparition du couplage Spin Orbite). Le moment magnétique est alors essentiellementent déterminé par le moment de Spin, le cas le plus flagrant de cette situation étant constitué par l'ion Mn3+. A l'inverse, les ions de Terres rares seront moins sensibles au champ cristallin. Le moment orbital est préservé et reste comparable à celui de l'ion libre avec un couplage Spin-Orbite opérant.
A ce stade, nous n'avons introduit que les ingrédients minimaux permettant d'expliciter la nature et l'amplitude du moment atomique de l'atome isolé ou lié au sein d'un édifice. Les interactions d'échange ferromagnétique apportent un troisième terme d'énergie déterminant pour les propriétés magnétique des matériaux ordonnés. Le champ cristallin, associé au couplage Spin-Orbite se manifeste également par l'existence de l'anisotropie magnétocristalline.
mise à jour le 22 novembre 2018
 Laboratoire de Génie Electrique de Grenoble
Laboratoire de Génie Electrique de Grenoble
