Nos sites
eServices
 Connexion
Connexion
 Connexion
Connexion

Les interactions d'échange ferromagnétiques s'exercent dans les matériaux présentant des atomes dotés d'un moment magnétique permanent. Lorsque les distances entre atomes magnétiques sont suffisamment petites (de l'ordre de l'Angström), donc au sein de la matière condensée, les orbitales électroniques interagissent, donnant lieu à l'état magnétiquement ordonné présenté par les matériaux dits ferromagnétiques.
Le matériau ferromagnétique présente une polarisation magnétique même en champ nul, polarisation qualifiée pour cela de spontanée. Celle-ci est la manifestation macroscopique du fait que les moments atomiques ont tendance à s'aligner parallèlement les uns aux autres, réalisant une mise en ordre que l'on peut comparer à la mise en ordre géométrique (cristallisation) caractéristique elle aussi de l'état solide. De la même manière qu'une augmentation de température conduit à la destruction de l'arrangement géométrique (température de fusion), une augmentation de température conduit à la destruction de l'ordre directionnel des moments magnétiques (obtenue à la température de Curie notée Tc) pour laquelle la polarisation spontanée disparaît.
L'existence d'une polarisation spontanée confère aux ferromagnétiques (et aux matériaux de comportements macroscopiquement apparentés comme les ferrimagnétiques) des qualités irremplaçables pour les applications. On compte finalement peu d'éléments concernés par ce comportement. Ceux-ci appartiennent aux deux grandes familles que sont les Terres rares (Sm, Pr, Nd...) où les électrons responsables du magnétisme appartiennent à la sous-couche 4f et les métaux de transition (Fe, Ni, Co) où les électrons responsables du magnétisme appartiennent à la sous-couche 3d. Les composés et alliages réalisés à partir de ces deux familles constituent donc la base des matériaux magnétiques utilisés en Electrotechnique.
Où Si et Sj désignent les moments de Spins magnétiques associés aux deux atomes, Jij désignant l'intégrale d'échange entre les atomes i et j. En fonction de la distance entre atomes, Jij présente un caractère oscillant centré sur la valeur nulle et d'une façon générale, la valeur de Jij décroît vite avec la distance, de sorte que l'énergie d'échange ne s'exerce en première approximation qu'entre atomes voisins, son signe déterminant la nature de la loi de comportement de la substance : positive, Jij détermine le comportement ferromagnétique ; négative, Jij détermine le comportement antiferromagnétique qu'on ne détaillera pas.
On peut proposer une alternative simplifiée à la formulation précédente en raisonnant sur le cas d'une substance composée d'un seul élément magnétique. Le facteur intégrale d'échange est le même pour toutes les paires d'atomes proches voisins et ne sera plus indicé. Par ailleurs, les moments magnétiques i et j portés par les atomes étant eux-mêmes étroitement liés aux moments de Spins i et j, on exprimera finalement l'énergie d'interaction sous la forme
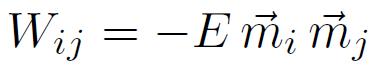
On obtient alors l'énergie d'un moment magnétique i plongé dans un champ d'induction appliqué e et entouré de Z proches voisins de moments magnétiques j , 1<j<Z :
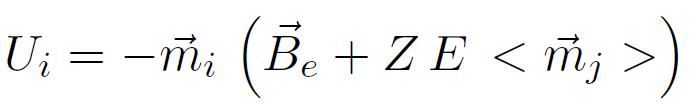
Dans l'approximation du champ moléculaire on fait l'hypothèse que 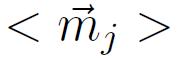
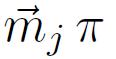
En notant : 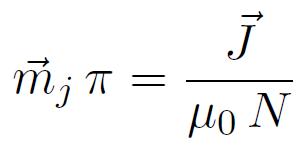
où N désigne le nombre d'atomes porteurs de moments par unité de volume, on obtient :
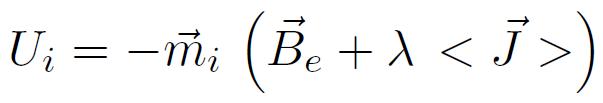
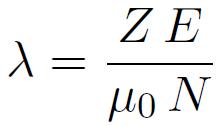
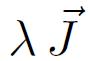 proportionnel à la polarisation du matériau. C'est ce champ interne que Pierre Weiss a appelé le champ moléculaire,
proportionnel à la polarisation du matériau. C'est ce champ interne que Pierre Weiss a appelé le champ moléculaire, 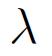 étant le coefficient de champ moléculaire.
étant le coefficient de champ moléculaire.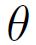 entre l'orientation des moments et le champ appliqué est régi par une densité de probabilité:
entre l'orientation des moments et le champ appliqué est régi par une densité de probabilité: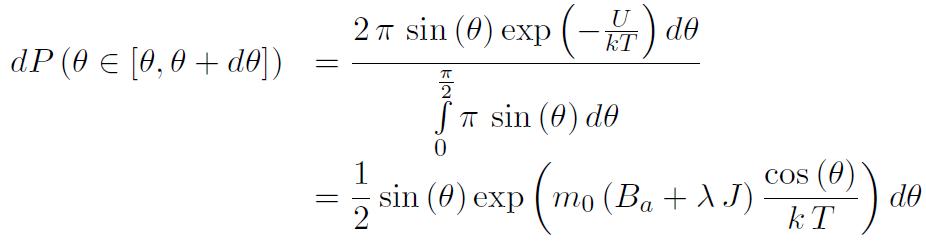
où k=1,3807.10-23 J/° désigne la constante de Boltzmann et m0 l'amplitude du moment atomique. On obtient une polarisation d'amplitude réduite :
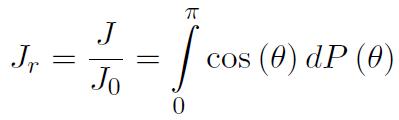
où 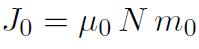
désigne la polarisation spontanée correspondant à l'alignement de tous les moments individuels, situation observée en l'absence d'agitation thermique, donc à T = 0 °K. En posant 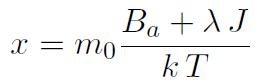
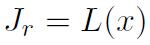
Où 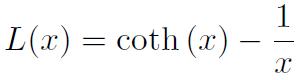
On peut également exprimer Jr en fonction de x, soit :
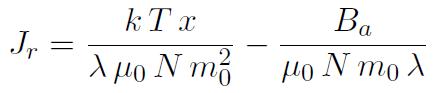
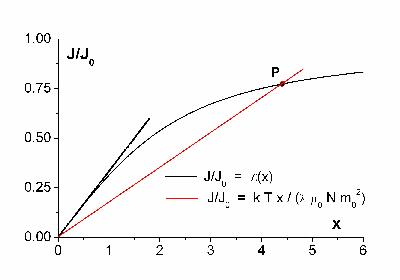
On obtient ainsi une deuxième relation qui, conjuguée à la loi Jr=L(x), permet d'établir la valeur de la polarisation pour un champ Ba et une température donnés. L'observation d'une polarisation spontanée (donc pour Ba=0), matérialisée par le point d'intersection P de la figure 1, n'est possible que si la pente de la droite :
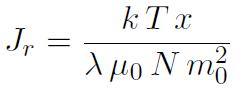
est inférieure à 1/3 (pente initiale de la fonction de Langevin), de sorte que la température de Curie vérifie:
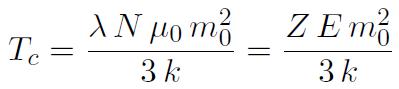
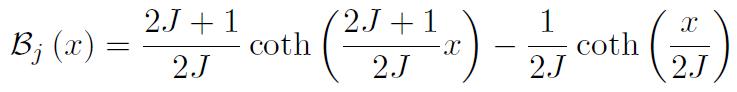
La température de Curie s'exprime alors plus exactement sous la forme
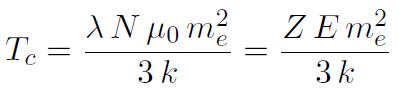
où : 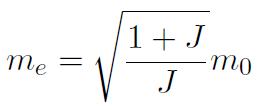
désigne le moment effectif. La philosophie du calcul et les ordres de grandeur restent inchangés par rapport à l'approche classique.
Le modèle de Weiss que l'on vient de décrire s'applique à priori pour des matériaux où les moments magnétiques sont localisés sur les atomes, ce qui est le cas des éléments de Terres rares mais n'est pas le cas des éléments de transition 3d (Fer, Ni, Co) à l'état métallique, caractérisés par un magnétisme itinérant et pour lesquels des modèles plus sophistiqués sont requis. On constate cependant que la théorie du champ moléculaire de Weiss donne des résultats très corrects pour le Nickel, le Cobalt et le Fer (cf figure 2), avec une courbe calculée basée sur une fonction de Brillouin 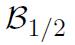
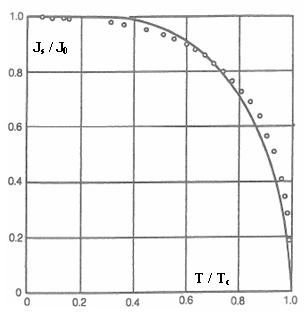
Figure 2 : Evolution de la polarisation spontanée avec la température dans le cas du Nickel ( J0 = 0.64 T, Tc = 631 °K). La courbe correspond à la formulation théorique, les points aux relevés expérimentaux
mise à jour le 22 novembre 2018
 Laboratoire de Génie Electrique de Grenoble
Laboratoire de Génie Electrique de Grenoble
